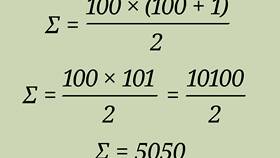Сумма модулей чисел - это важная математическая операция, часто используемая в различных расчетах. Модуль числа (абсолютная величина) всегда представляет собой неотрицательное значение, независимо от знака исходного числа.
Содержание
Определение модуля числа
| Число | Модуль числа |
| 5 | 5 |
| -3 | 3 |
| 0 | 0 |
Формула суммы модулей
Сумма модулей нескольких чисел вычисляется по формуле:
|a₁| + |a₂| + |a₃| + ... + |aₙ|
где |a| - модуль числа a
Пошаговый алгоритм вычисления
Определение модулей каждого числа
- Возьмите первое число из набора
- Если число отрицательное, измените его знак на противоположный
- Если число положительное или ноль, оставьте без изменений
- Повторите для всех чисел в наборе
Сложение полученных значений
- Сложите все модули чисел
- Проверьте правильность вычислений
- Результат всегда будет неотрицательным числом
Примеры вычислений
| Набор чисел | Вычисление | Результат |
| 4, -2, 7 | |4| + |-2| + |7| = 4 + 2 + 7 | 13 |
| -5, -3, -1 | |-5| + |-3| + |-1| = 5 + 3 + 1 | 9 |
| 0, 6, -4 | |0| + |6| + |-4| = 0 + 6 + 4 | 10 |
Свойства суммы модулей
- Результат всегда неотрицательный
- Сумма модулей ≥ модуля суммы чисел
- Для любых чисел a и b: |a + b| ≤ |a| + |b| (неравенство треугольника)
- Сумма модулей противоположных чисел удваивает их абсолютное значение
Практическое применение
Где используется сумма модулей
- Вычисление среднего абсолютного отклонения в статистике
- Определение расстояний в геометрии
- Анализ погрешностей измерений
- Решение уравнений и неравенств
Важные замечания
- Порядок чисел не влияет на результат
- Сумма модулей всегда ≥ суммы самих чисел
- Для положительных чисел сумма модулей равна их обычной сумме
- При работе с дробями и десятичными числами правила те же